The Gravity of the Situation

The theory of general relativity burst into public awareness when observations made off the west coast of Africa during a 1919 solar eclipse confirmed one of Albert Einstein’s most astonishing assertions: that large masses, like the sun, warp space and thus bend the path of light. Legend has it that Arthur Stanley Eddington, the British astronomer who corroborated the theory when he measured the angle of starlight deflection, was asked whether it was true that only three people in the world understood relativity. After a moment, Eddington supposedly replied: “Who’s the third?” Announcing relativity’s vindication, The New York Times had to explain who Einstein was (“a Swiss citizen,” it laconically offered) and, in the lead paragraph of its account, bluntly acknowledged that “it is not possible to put Einstein’s theory into really intelligible words.”

A century later, everything seems to have changed. If you believe the jacket copy, for the price of a book you now can understand relativity, quantum physics, cosmology, or pick your subtopic: black holes, subatomic particles, symmetry, electromagnetism, string theory, gravitational waves, the Higgs boson, quantum entanglement, the Big Bang, and on and on. Duck into any bookstore or search any online bookseller and you’ll find an ever-expanding section of popular offerings standing ready to initiate inquisitive readers into the latest scientific mysteries, and all without the need to understand math or have any feeling for experiment. (A growing number of websites offer the same.) It’s cheap. It’s easy. It’s entertaining.

It’s bogus.

Or so I have come to believe, many years after discovering Banesh Hoffman’s classic, The Strange Story of the Quantum (1947), while taking high school physics in the late 1950s. I’ve read hundreds of similar books since then, and they’re not all bad. Most are readable, even sprightly, often cloaked in infectious good spirits. The trouble is, familiarity breeds suspicion. If you try to keep up with developments, the stories become so well worn that, in succeeding books, you begin to notice subtle difficulties that the authors gloss over. After some time, you might begin to suspect that the accounts they provide are deflections from reality, like starlight around the sun, because the popularizers are loath to admit that a subject that enraptures them has loose ends, vague contours, or gaping holes. These writers’ longing to instill in readers their own passion and even reverence for the science often overwhelms their prudence. Instead of giving their readers the whole truth, popularizers take to papering over theoretical weaknesses with jargon, fuzzy talk, or even outright silence. Such obfuscations and omissions apply to some of the most basic elements of physics, like gravity, the Big Bang, the nature of space, the properties of subatomic particles, even how to measure and meaningfully describe the basic architecture of the universe.

THE PROBLEM OF GRAVITY

Have you ever thought hard about gravity? Chances are you’ve accepted it without critical reflection, but what is it, and how does it work?

Aristotle had a hypothesis: things do what is natural to them. Some essence within all things, almost akin to a desire, moves them. Heavy things, like apples, dishware, and babies learning to walk, fall to the ground because they want to go downward, because they are of Earth and it’s in their nature to return—unlike, say, smoke, which Aristotle thought to be possessed of something called “levity,” gravity’s opposite. Levity made smoke want to curl upward.

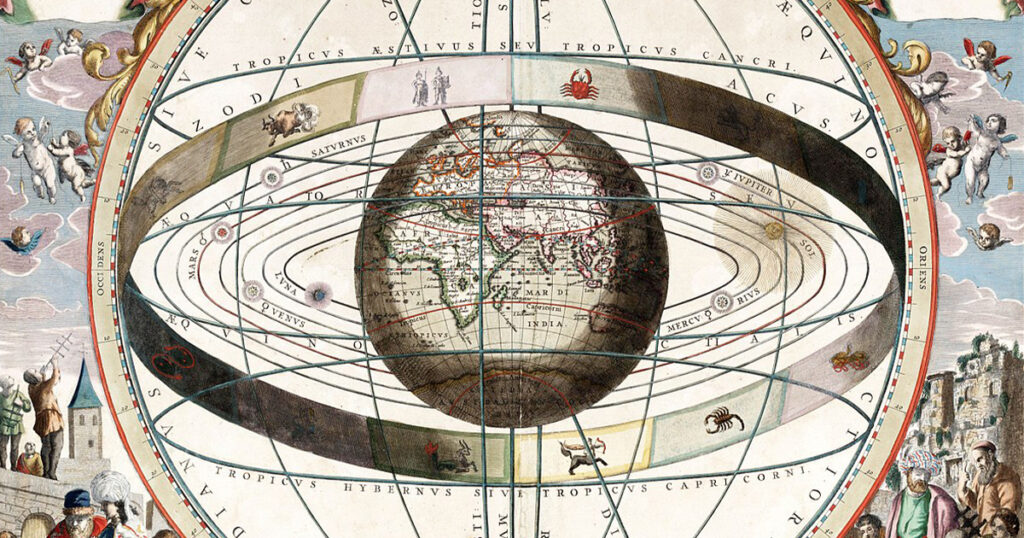
To the ancients, the motion of moon, sun, and planets had no connection to the force we know as gravity or to the desire of heavy things to get to the center. Astronomers believed that celestial bodies inhabited a separate realm. Embedded in concentric shells, they revolved around a stationary Earth (thought to be the center of the universe) in perfectly circular orbits. Unfortunately for the ancients, orbital paths are not circles, and Earth is not at their center, so sky watchers encountered well-known anomalies, such as retrograde motion: the planets periodically reversed direction and circled backward before resuming their forward course. To “save the appearances”—that is, to account for what they actually saw—astronomers were compelled to confect a dizzying system of circles on circles, culminating in the second century CE in the jaw-dropping epicycles of Ptolemy. Picture a child in a fairground running round and round a wooden horse on the platform attached to a spinning merry-go-round. You could more or less trace the movement of a “wandering star” that way, but no one could point to a celestial mechanism that explained such an absurdly complex set of motions. Nevertheless, Ptolemaic epicycles persisted for more than a millennium until new technologies, better observations, and an awakening scientific spirit dared to challenge core assumptions. In the 16th century, the Copernican revolution swept away the old theories, but it would be another century before Isaac Newton provided a better, more comprehensive one.

In his 1687 masterwork, Philosophiae Naturalis Principia Mathematica (the underlying theory for which he had developed two decades earlier while quarantined at home during an outbreak of bubonic plague), Newton proposed gravity as a force pervading the universe. It works not just on Earth but throughout the cosmos, accounting for the orbits of the moon and planets in mathematically specified ways. Among his principal achievements, Newton showed that the force of gravity is inversely proportional to the square of the distance: a planet twice as far from the sun as Earth would feel only one-quarter the sun’s gravitational force. He also proved that equations describing such a force require planets to ride elliptical, not circular, orbits around the sun, a geometry that Johannes Kepler had discovered more than three-quarters of a century earlier. The result of Newton’s intellectual labors was a coherent system that accounted for celestial phenomena (like the actual path of the planets) and accurately predicted eclipses, the existence of theretofore-unknown planets, and the periodic return of comets.

The Newtonian system reigned for more than two centuries (and it’s still in hardy use today), but it does not accommodate all observed phenomena. It notably errs, for example, in describing the orbit of Mercury. Newton assumed that gravity extends instantaneously throughout all of space, even though, as we now know, nothing can travel faster than the speed of light. He viewed space as a fixed and unmoving container in which time methodically and ceaselessly ticks its rhythmic tock from past to future, the same rate for everyone and everything everywhere.

Nevertheless, from the time Newton gave gravity the central place in his system, the observed motions of planets depended on an enigmatic “force.” It mystified Newton himself: how could gravity emanate from matter to corral something across the vast distances of space? As Newton wrote to Cambridge theologian Richard Bentley in 1692, “the cause of gravity is what I do not pretend to know.” Elsewhere in their correspondence, he elaborated:

It is inconceivable that inanimate brute matter should … affect other matter without mutual contact. … That gravity should be innate, inherent, and essential to matter, so that one body may act upon another at a distance … is to me so great an absurdity that I believe no man who has in philosophical matters a competent faculty of thinking can ever fall into it.

It took Einstein to come to the rescue, or so say our popularizers. Relying on two centuries of scientific observations, experiments, and mathematical developments, Einstein proposed two revolutionary theories: special relativity (1905) and general relativity (1915). Though Newton’s mathematics still apply for everyday events, Einstein overturned Newtonian assumptions and provided a radical and comprehensive physical explanation for the way things work.

What kind of property is it, then, this gravity business, that allows unconnected bodies to attract each other remotely? What is it that leaps out from the sun to lasso Earth into permanent orbit? How does Earth pull you down when you dive off a board into a swimming pool? Einstein solved the mystery of force at a distance by rejecting it. According to him, there is no such property. Gravity is not a force. The gravitational phenomenon (or the matter in which it resides) is neither strongman nor sorcerer; it is a geometrician and sculptor. It doesn’t reach, pull, or grab. It molds the very contours of the cosmos in which things move, like a highway engineer banking a roadway as it winds through a mountain pass. To account for gravity, according to general relativity, we must conclude that mass warps space and time. Or as the American physicist John Archibald Wheeler pithily put it: “Matter tells space how to curve. Space tells matter how to move.”

In other words, because space curves, you need not point to a force called gravity to explain the path of a moving object. It’s not a force that curves a batted baseball down to Earth in a parabolic trajectory; it’s just the ball following the shortest possible route in the curvature of what has come to be known as “spacetime.” Gravity is merely an artifact of the geometry of the cosmos.

If you don’t quite grasp this, I can offer two explanations that physics popularizers have relied on. The first is to think of how to get somewhere on Earth by the shortest route. If Earth were flat, the shortest route between, say, London and San Francisco would be a conventional straight line as plotted on a page in an atlas. On the usual North American view of a world map, it would take you across the Atlantic hundreds of miles south of Greenland and into the United States north of Boston, then across Denver, and west to San Francisco. But because the Earth’s surface is curved, the shortest distance is actually a great circle route, which uses the center of the Earth as its point of reference. Traveling from London to San Francisco along a great circle, you pass over southern Greenland and arc over Hudson Bay and much of Canada, entering the United States in Montana, and then south to San Francisco. Analogously, that’s what happens, said Einstein, in four-dimensional spacetime, although we can’t picture it. The presence of sufficient mass, like the sun, curves time and spatial dimensions into a four-dimensional spacetime, just as a rounded globe curves onto its three-dimensional surface a two-dimensional map, thus altering the trajectories of everything seeking the shortest path. We orbit the sun not because the sun tugs at us but because Earth is caught in a curved path.

The popularizers’ second way of understanding relativity’s take on gravity is to picture four friends holding taut each corner of a bed sheet. Take a bowling ball and place it in the center of the sheet. Observe what happens: the flat sheet dips in the middle toward the floor, and the bowling ball sits in the depression, sunk below the sheet’s plane, a two-dimensional surface curved into three dimensions. Put a marble on the sheet, and it will follow the lines of the sheet into the well where the bowling ball sits. The marble is responding to the geometry.

Relativity, we’re told, has passed every test to which it’s been subjected during the past 100 years; its predictions have all been borne out. It accurately accounts for the shifting orbit of Mercury, and without incorporating relativistic principles, our entire GPS system would fail. No matter how bizarre it seems to minds that evolved on the surface of a round planet, relativity accounts for the observed facts. But it’s only the mathematics of relativity that has improved on the Newtonian equations. As an explanation of physical phenomena, relativity scarcely resolves Newton’s perplexity. Gravity remains unexplained.

The physics popularizers tell us that gravity is not a property of matter (or mass) that attracts things through space. It is, instead, a property of matter that “bends” or “curves” the space in which it sits. But how is our understanding enriched by substituting a mysterious bending or warping for a mysterious pulling? What is it about matter that allows it to curve space? How can three-dimensional space be curved, along with time, into a fourth dimension? Why is motion an artifact of non-Euclidean geometry? On these questions, the popularizers are silent.

Let’s return to the bowling ball in the sheet. Alas, this “analogy,” offered by many popularizers over the years, depends for its insight on engaging your lifelong Newtonian intuition about gravity as a tugging force. The only reason the marble drops into the depression in the middle of the sheet is that old-fashioned gravity-as-a-force pulled it there. This image of the ball in the sheet gives us no clue to how mass warps spacetime.

Nor does it explain motion. Why does an object move when it is sitting in curved space? Place the marble on a table top. It is in a “gravitational field”: the massive Earth has warped space, creating a curve in spacetime surrounding the table and the marble. The marble is unmoving while sitting on the table because an electrostatic force, much more powerful than gravity, prevents it from plunging through the space between the atoms of the wooden surface. But if you hang the marble just beyond the table’s edge and release your hold, it falls. Not only does it fall, it also accelerates as it drops. Why does curved space cause the marble to move at all, much less to gain speed? If no force is pushing or pulling on it, what makes it go faster?

Perhaps physicists have an explanation for motion generated by a curvature of space, but the physics writers haven’t provided it. Most ignore the issue completely. British science writer Brian Clegg, one of the best of the contemporary popularizers, does pause to consider the question. He agrees that the bowling-ball-in-sheet analogy is circular: since it uses gravity to explain gravity, it “has no value.” How, then, does the warping cause motion? Because, Clegg writes in his 2012 book Gravity, even if the marble is stationary in space, it is moving through time, always going from past to future. Mass warps spacetime, not just space. Hence the dropped marble “has to start to move.” This seems more a semantic trick than a physical explanation, the word move accreting a new definition, its meaning warped by the need to supply an answer to a mystery yet unresolved. But even that explanation is only partial. It does not extend to the full phenomenon. For the dropped marble does not merely fall; it travels downward at an accelerating rate. (Caught in the grip of Earth’s gravity, you’ll drop increasingly quickly, every second by 32 feet more than the previous second. Step off a ledge, and after a second, you’ll be falling at a rate of 32 fps; at the end of two seconds, at 64 fps; and so on at an ever-increasing speed—that is, until you reach “terminal velocity” because of air resistance near Earth’s surface.) Motion and acceleration are different. Moving in time while sitting still in space doesn’t speak to the marble’s accelerated motion.

The math of relativity works, but the popular explanation folds in on itself, like the epicycles of yore. The only writer I’ve found who acknowledges this problem is science journalist Richard Panek, who writes in The Trouble With Gravity (2019), “Nobody knows what gravity is, and almost nobody knows that nobody knows what gravity is except for scientists, and they know that nobody knows what gravity is because they know that they don’t know what gravity is.”

THE PROBLEM OF ORIGINS

The length of these musings on gravity should not be taken to imply that it is the principal arena in which popularizers shirk their duty. They do worse, though perhaps not nearly so obviously, in telling other stories about the nature of reality.

Take the Big Bang. Everyone knows that it gave birth to our universe. What exactly banged, though, is another story. Just before it happened, whatever there was and wherever it was is characterized as an “infinite singularity.” American astrophysicist Neil deGrasse Tyson told a television audience, “Everything that exists today was in the same place at the same time.” Heard one way, Tyson is suggesting that everything was curled up tight. This is what hasty popularizers often take to be the case. Thus, British historian Felipe Fernández-Armesto writes in Out of Our Minds (2019), “the Big Bang Theory … describes infinitesimally compressed matter, already there before the Bang redistributed it, expanding into the recognizable universe.” But if matter in its present form (quarks and electrons and suchlike) was already there, infinitely packed, then the singularity should have been the ultimate black hole, from which, popularizers tell us, nothing can escape. That’s a problem. Heard another way, Tyson might have meant that matter existed in some other form—pure energy, perhaps. Meaning what? Created how?

THE PROBLEM OF SPACE

For most of us, our naïve view of space is likely the same as Newton’s: that it is just a very large room, an open container in which we are situated, a stage on which things happen. But the popularizers tell us that despite our intuition, space is not uniform or fixed. For one thing, in a fraction of a second after the Big Bang, space “inflated” (for an additional fraction of a second). If the inflation was not just stuff being pushed outward into preexisting space, then what is the stuff that inflated? Swedish-American physicist Max Tegmark, in Our Mathematical Universe (2014), refers to it as an “inflating substance.” (Should we call it inflaturium? ) Space also expands, amazingly enough, even faster than the speed of light. The explanation for this is an apparent contradiction: that nothing can exceed the speed of light through space, but when space itself expands, that’s different, even when it drags huge chunks of mass, like galloping galaxies, along with it. So space is indeed something, since it appears to stretch, but not enough of a thing that it can be ticketed for violating the universal speed limit.

But space doesn’t only expand and curve; it can also shrink—inflaturium becoming deflaturium. This property is courtesy of the special theory of relativity, according to which only the speed of light is invariant. People everywhere, no matter how slowly or fast they are going, experience light moving at the same unchanging speed. If you are on a train traveling at 100 miles per hour and you throw a ball at 25 miles per hour to a passenger ahead of you in your railroad car, an observer on the ground would measure the speed of the ball at 125 miles per hour relative to the track as the train whizzes past. The measured total speed is additive. Not so with light. Shine a flashlight forward in the same railroad car. The observer outside will not clock the beam from your flashlight at the speed of light plus 100 miles per hour. The measurement would instead show the light beam traveling at precisely the speed of light, no faster, no matter how quickly the train is barreling along. It’s as if you stepped onto a moving conveyor belt at the same moment a companion stepped alongside you onto a parallel belt moving more slowly; you both walk at the same speed, and yet you both arrive at the other end together. Sounds impossible, right? The only way it could happen is if, as you move faster, time dilates (gets slower, contra Newton), the path you are following shrinks, and your length contracts in the direction of motion. All this is not merely counterintuitive. It is astounding! What is space that it can curve and stretch and shrink and ripple, as the recent direct detection of gravitational waves has now confirmed? Our popularizers give us only studied silence.

THE PROBLEM OF FIELDS

One of the most important concepts in all of physics, say many physics writers, is the “field”: electromagnetic, gravitational, quantum, Higgs. As usually defined, a field is a physical quantity with a specific value at every point in spacetime. But fields in physics are not merely descriptive, like temperatures on a weather map. They are said to be physical entities, possessing such characteristics as momentum and energy. You will read that many particles (photons, the Higgs boson) are “disturbances” in their respective fields. But don’t expect to find extended discussions of fields in any popularization. Are they real or only a mathematical construct for some underlying reality? If they are real, what is their physical form? Do they get in the way of each other? Our physics writers aren’t saying.

THE PROBLEM OF PARTICLES

For purposes of calculation, physicists postulate that particles, the most elementary objects currently known, are dimensionless, pointlike entities. But how do dimensionless things bounce off each other, respond to forces, and serve as the building blocks of a universe with extended substances, which by their nature are divisible? And how can elementary particles (quarks, for example), made up of nothing but themselves, be extended in space? There are six kinds of quarks, each one with a different mass. Are they made up of the same little blobs of filler, with more or less of it as suits? Are there different varieties of stuff? And if so, isn’t the stuff itself simpler? Physicists may hypothesize about these things, but the travel guides to our universe are keeping mum. Perhaps it doesn’t matter: recent literature suggests that particles aren’t particulate at all, despite the cute illustrations in popular books, nor are they fully wavelike. And just how do various forces (strong, weak, electromagnetic) bind particles to (or repel them from) each other? The mechanism is occasionally hinted at but is almost entirely occluded by the word force.

THE MEASUREMENT PROBLEM

Even casual readers know that the quantum world acts very differently from the one we experience. Our world is continuous—in moving from here to there, an object encounters each point in between. Not so, we read, in the quantum arena, where subatomic particles take “quantum jumps,” somehow going from here to there without passing by any of the in-betweens. Indeed, there’s a fundamental problem with the very concept of fixing a particle’s location. According to the predominant view of quantum reality (the “Copenhagen interpretation”), particles actually have no location (somehow, are not really “there”) until their location is measured. You’re likely to find that an odd conclusion. Einstein did, asking mordantly whether the moon exists only when we look at it. If I may risk a nonphysical analogy, in The Federalist No. 37, James Madison said that all new laws enacted by legislatures are “equivocal until their meaning [is] liquidated in actual cases”—that is, until “measured.” That doesn’t mean that laws don’t exist until a case arrives in court or that the legislators didn’t have a purpose in enacting them.

Physicists nevertheless have a way of describing the probable location of these things that, by their own reckoning, are not there. They use a particle’s “wave function.” Unhappily, the wave function has almost as many nonmathematical definitions as there are popularizers trying to explain it. In essence, it is a mathematical description of the probability of finding a particular particle at any particular point in space. When a particle’s location is actually measured (observed), its wave function “collapses” instantaneously—a theoretical problem for many physicists. Another problem, this one for readers, is how a probability of location is computed for a particle that has no location until it is measured.

One solution to the mystery of a particle just materializing into place is that it doesn’t. Observing a quantum event does not collapse the wave function, say proponents of this view, but splits it, giving birth to a multitude of new universes wholly inaccessible to us, one for every possible outcome. In your universe, you may have just lost the lottery for the 100th time, but in a newly branched universe, an identical copy of you may have won a fistful of dollars. “Measurement” and “observation” are contested terms, as theoretically a measuring instrument can register the motion of a particle without a scientist’s seeing or being aware of the measurement. So it’s not clear how often proponents think this splitting happens, but it seems safe to say it occurs several gazillion times every second, given the number of possible locations a particular particle could have had and the number of particles that go bump at each instant. That’s a lot of parallel universes. This account is known as the “many-worlds interpretation” and is taken seriously by many physicists today. Still, I don’t know of a popularizer who has raised the question of where all the extra matter required to build all of these alternate universes comes from, or what such a supposition does to universally accepted conservation laws. Ptolemy had nothing on our modern many-worlders. Appearances need not be saved that way. In Where Does the Weirdness Go? (1996), British-born astrophysicist and science writer David Lindley, one of the few popularizers who provide both clarity and depth, has suggested that by taking account of not only how a particle acts when measured but also what an instrument does when taking a measurement, we’ll see that there was never really a problem to begin with.

THE POPULARIZATION PROBLEM

Thirty years ago at a conference in Sweden, American science journalist John Horgan listened with mounting incredulity as Stephen Hawking and other prominent physicists speculated wildly on quantum cosmology. A few years later in The End of Science (1996), Horgan admitted to repressing an “instinctive feeling of preposterousness” because, after all, these were “terribly smart people” who “would not waste their time on trivial pursuits.” For a while, he had resolved to make the ideas “sound plausible, to instill awe and comprehension instead of skepticism and confusion in readers.” But in his book, he acknowledged the importance of airing his suspicions that whatever all the smart people were doing, it wasn’t science. Attempting to explain it as if it were, Horgan concluded, is simply “dishonest.” I say it’s past time for popularizers to realize, like Horgan, that they’re not writing for physicists; they’re writing for the rest of us.

Recently, a few have heard the call. American astrophysicist Adam Becker, in What Is Real? (2018), takes a hard look at the Copenhagen interpretation, exposing a fault line that goes beyond mere physics to the very ways we describe reality, raising serious doubts about the validity and utility of the orthodox quantum story that we cannot know the world “independently of our perceptions.” In Lost in the Math (2018), Sabine Hossenfelder chides physicists for faulty motivations and theorizing, particularly in the claim that “beauty” is a test of validity (though she herself can be mystifying when she strays into the chitchat of the trade). Jorge Cham and Daniel Whiteson, in We Have No Idea (2017), forthrightly and lightheartedly detail the vast number of quandaries that confront physicists even in well-developed theories. With varying degrees of clarity, some other writers have challenged the conventional wisdom or gone beyond explaining it in conventional terms.

Even so, most popularizations still fall short in a number of predictable ways.

IGNORING THE MATH

I’m not suggesting that we amateur inquirers are prepared to learn differential calculus or knot theory, but writers do need to explain more actively the role that math plays in shaping theories and running experiments, and how mathematical operations give rise to the popular accounts we read.  For example, many writers offer a sentence or two about German physicist Karl Schwarzschild’s “exact solution” of the general relativity equation shortly after Einstein published the theory. It would be useful to know how the equations are devised, what Einstein’s equation postulated, why it was unsolved, and what “solving” it suggests about the universe. In his latest book, The Dream Universe (2020), David Lindley suggests an approach to discussing mathematics, but it is not his main point and he does not flesh out the idea.

FORGETTING THE AUDIENCE

Lately, many popularizations seem to be written for physicists rather than lay readers looking for enlightenment. That’s perhaps because more and more of the popular accounts are written by physicists themselves, pushing their own interpretations. Sometimes the authors are simply showing off, suckered by jacket praise from fawning blurbists (almost always fellow physicists) into surfeiting the unprepared reader in dreary and indigestible detail. From the many offenders, I’ve selected three at random: Lawrence Krauss in The Greatest Story Ever Told—So Far (2017), Gavin Hesketh in The Particle Zoo (2016), and Steven S. Gubser in The Little Book of String Theory (2010). Although all three authors are physicists, they offer their books to a general audience.

Consider this passage from Krauss, a well-known physicist who retired from Arizona State University last year, showcasing his cryptic but pervasive strutting:

He thought perhaps the photon could be the neutral member of a Yang-Mills-type set of three gauge particles required by treating isotopic spin as a gauge symmetry, with the charged versions conveying the weak interaction and being responsible for mediating the decay of neutrons.

This one from Hesketh, a young CERN researcher and professor of astronomy and physics at University College London:

If this Higgs field exists, then it is possible to make the weak force work as a gauge symmetry. The W boson is a real gauge boson, and is naturally massless. But at some point in the very early universe, the Higgs field ‘turned on’ and broke the weak-force gauge symmetry. Through interacting, or ‘sticking’ to the Higgs field, the W boson acquires some mass. This is the loophole: the mass of the W is not a property of the W boson itself—which is not allowed by the symmetry—but is a result of the interaction of the W boson with the Higgs field. Because the weak-force gauge symmetry is broken, the symmetry between the different states of the weak charge is broken also, and we can tell the difference between the electron and the neutrino, for example.

And this from Gubser, a professor of physics at Princeton who died last year in a climbing accident:

[I]nteractions [of D3-branes and strings] can be made stronger or weaker by changing a parameter of that gauge theory. If you make the interactions very strong, then thermal states are best described in terms of a black hole horizon that surrounds the D3-branes. This horizon is hard to visualize, because it is an eight-dimensional hypersurface in a ten-dimensional ambient geometry.

FEIGNING CONSENSUS

Popularizers tend to treat facts as if they are part of an unfolding reality in a detective story. Once discoveries are made, we’re meant to believe, everyone accepts not only the bare experimental observation but also the conceptual scaffolding that may later be attached. But disagreements often derive from the physicists’ own inability to explain themselves. Niels Bohr, one of the principal architects of quantum theory, was notoriously obscure, as recent popularizers have recognized. Sometimes the disagreements spring from differing views on what the physicist’s job really is. Bohr once said that “it is wrong to think that the task of physics is to find out how nature is. Physics concerns what we can say about nature.” Einstein felt otherwise.

FAILING TO WRITE CLEARLY

To be fair, as German theoretical physicist Werner Heisenberg put it, sometimes “our words don’t fit.” The subject is difficult, its principles not fully understood or worked out. It’s unsporting, after all, to shoot the pianist who’s doing his best. But sportsmanship does not require uncritical praise,  just as cracks in the theoretical edifice can’t always be repaired by  wallpaper. Most popularizations either fail to define significant concepts or ignore their apparently controversial reality. Words such as space, mass, particle, field, and energy are tossed about as if their meaning is obvious and uncontested. When concepts are too daunting or not fully understood by the physicists, many writers paper over the mystery with obscure and fuzzy prose. Pick up, for example, any of the recent books purporting to explain the importance of the Higgs boson, newly discovered at CERN’s Large Hadron Collider in Geneva. The front of the bookstore is still waiting for the book that can do it.

If I’m wrong about the science in my much-too-brief summary, don’t blame the physicists. My quarrel is not with them and their work but with the meaning of it all as told by those who claim the authority to translate. By all means correct me. But only if you up your game. Meantime, I lament the strange obscurities of physics and, straining for the contradictions, am disappointed by the fuzziness, confounded by the jargon, dumbfounded by the silences, enchanted by the whoppers, and too addicted to quit.