The Uncertainty Principle
In an age of profound disagreements, mathematics shows us how to pursue truth together

Humans crave certainty. We long to know what will happen, what to believe, and how to live. This desire drives some of us to depths of soul-searching and heights of scientific inquiry. It drives others into the arms of authoritarians, who are all too willing to put our doubts, and our unquiet minds, to rest.
Philosophers have long warned that this desire for certainty can lead us astray. To think and learn about the world, we must be willing to be uncertain: to accept that we don’t yet know everything. In 19th-century Europe, when the urge for certainty was deepening national and religious divisions, Goethe wrote, “Nothing is sadder than to watch the absolute urge for the unconditional in this altogether conditional world; perhaps in the year 1830 it seems even more unsuitable than ever.” In the year 2020 it seems even more so. Many of us rely on political and tribal loyalties, dismissing any argument that could make us less certain of our views. At its worst, the desire for certainty crushes all subtlety and complexity under its heel.
Nietzsche called this desire to make the crooked straight the “will to truth.” In The Gay Science, he argued that for most of us, “nothing is more necessary than truth; and in relation to it, everything else has only secondary value.” But he suggests in another work, Beyond Good and Evil, that the will to truth is a vestige from a simpler time that has dominated the human psyche for far too long:
The Will to Truth, which is to tempt us to many a hazardous enterprise … what questions has this Will to Truth not laid before us! What strange, perplexing, questionable questions! It is already a long story; yet it seems as if it were hardly commenced. Is it any wonder if we at last grow distrustful, lose patience, and turn impatiently away? … We inquired about the value of this Will. Granted that we want the truth: why not rather untruth? And uncertainty? Even ignorance?
As Nietzsche writes, when our demand for certainty is frustrated—when the quest for truth is longer and stranger than we would like—we often give up. And just as some people turn to authority, others abandon even the idea of truth, deciding that there is no truth to be found.
Yet there is a middle way, between the extremes of absolute certainty and despair, that honors Nietzsche’s call to embrace uncertainty and ignorance, while maintaining our pursuit of meaning and truth.
Uncertainty can be a source of terror and anguish. It keeps us up at night. But it is also a generative force, and an invitation for deeper exploration. It forces us to earn our certainties, rather than buying them cheaply and wholesale. Indeed, a dynamic, honest search for truth requires us to regard uncertainty as an enduring companion rather than an enemy to be fled or vanquished. To wrestle with it, we must embrace it.
We can learn something about how to live with uncertainty from a field that few associate with it: mathematics. As we’ll see, mathematicians have been forced to struggle with uncertainty on many levels. This is true not just in probability and statistics—which address uncertainty quantitatively—but even in the bedrock of logic, arithmetic, and geometry, where most people expect rigid certainty to rule.
These struggles have given mathematicians a keen sense of the nature of truth: of when certainty can be achieved and when it is out of reach, as well as the boundless creativity we need to find it. There are lessons here for how all of us can pursue truth together, even in the face of the disagreements and uncertainties that surround us.
Like philosophy, mathematics was born of the basic human need to sort out the messiness of life, to bring order to chaos, to identify the underlying and often obscured forms that structure reality. In Philosophy 101, students study “proofs” of the existence of God, Descartes’ proof of the existence of the self (Cogito, ergo sum), and Kant’s transcendental deductions. Similarly, the gold standard in mathematics is a formal proof—a step-by-step demonstration that a statement follows unavoidably from an agreed-upon set of principles.
In 300 BC, Euclid proposed five postulates for geometry that let us prove things by drawing lines and circles with rulers and compasses and seeing how they intersect. Most of these postulates seem straightforward and incontrovertible. The first one, for instance, states that between any two points there is a straight line that connects them. Absolutely straight and narrow.
Euclid’s fifth postulate, however, is the source of a curious instability. It says that if two straight lines cross a third one but make angles with it that add up to less than 180 degrees, so that they lean toward each other, then those two lines cross somewhere above the third line, and not below it. If the sum of the angles exactly equals 180 degrees, then these lines are parallel, meeting only at infinity. This is certainly true in the geometry we are used to. Either two lines are parallel, or they tend toward each other and will eventually cross at one and only one point. (See Figure 1)
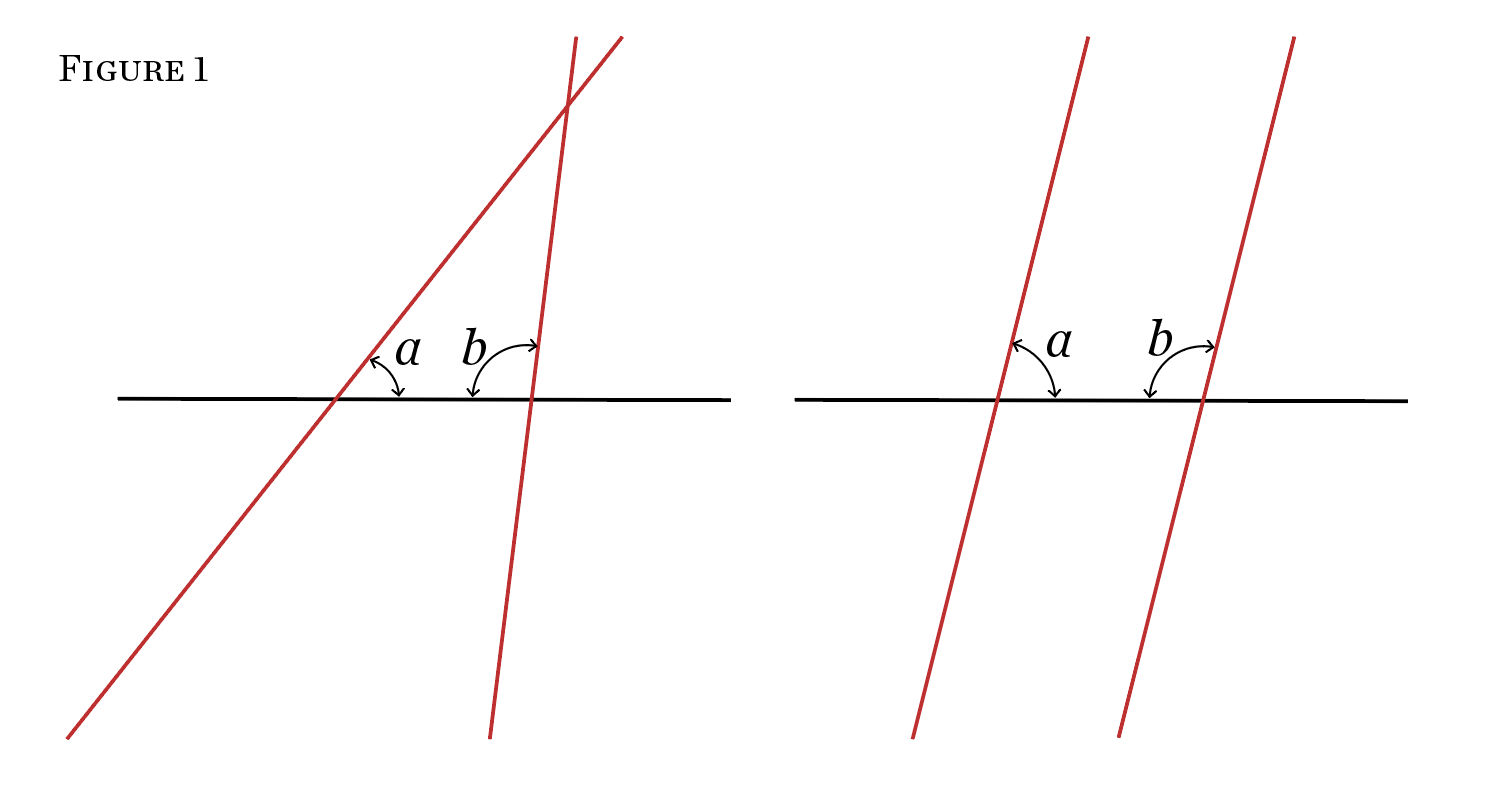
But for two millennia, mathematicians wrestled with the fifth postulate and struggled to prove it from the other four—or, like the poet and astronomer Omar Khayyam (1048–1131), to replace it with something simpler. Note that the question here is not just whether the fifth postulate is true. There is also the “metamathematical” question of whether it can be proved from more basic statements, or whether assuming it helps us prove other things in turn.
A revelation occurred in 1830, the same year that Goethe reflected on our urge for unconditional truth. There are alternate “non-Euclidean” geometries where Euclid’s first four postulates are true but the fifth is false. For instance, suppose we are moving on the surface of the Earth instead of on a flat plane. The closest thing we have to a straight line is a “great circle” such as the equator—the path we would follow if we proceeded straight ahead until we came all the way around to our starting point (and didn’t fall into the sea). A section of a great circle is the shortest path we can take between two points while staying on the Earth’s surface instead of tunneling under it. But no two great circles are parallel: any two great circles that cross the equator also cross each other twice, once in the Northern Hemisphere and once in the Southern, whereas Euclid’s postulate says they should cross once or not at all. (See Figure 2)
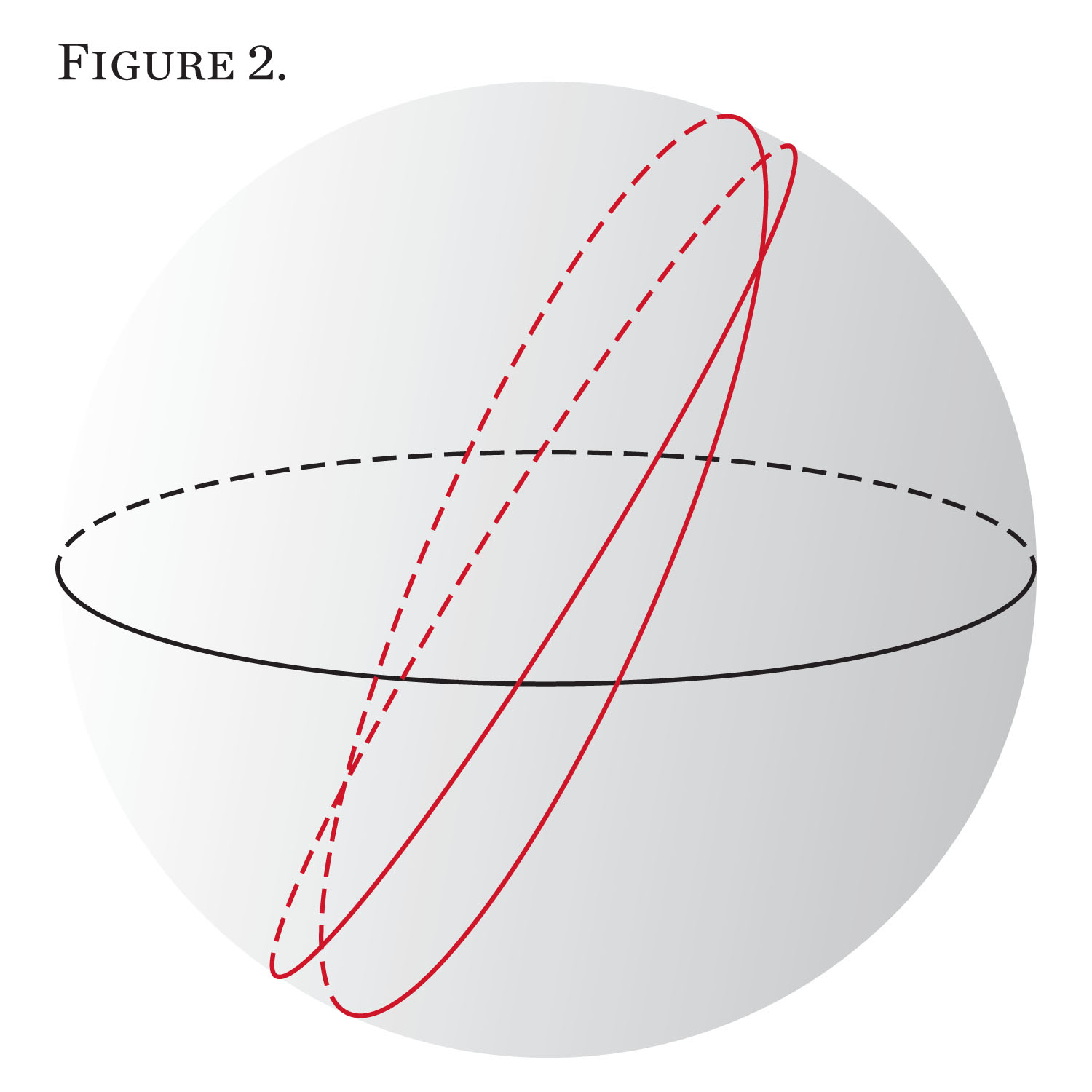
You might object that these are not lines at all. They are curves and decidedly not straight. Yes, but because of the Earth’s curvature, so is every line we draw on a map. The point is that if we adapt the phrase “straight line” to the curved world we live in, geometry works differently from the way it does on a flat piece of paper. There are more exotic so-called hyperbolic geometries where space spreads out rather than curving back on itself, and lines can fail to intersect, even if they start out moving toward each other.
So is the fifth postulate really true? In the flat worlds Euclid had in mind, yes. In curved worlds—including the universe we live in, as Einstein showed us—no. Where geometry is concerned, modern mathematicians are happy to accept the existence of alternate worlds in which different things are true. To be more precise, we think that a straight line is not a fixed object about which fixed things are true. It has different meanings in different worlds. All of these worlds have so much beauty, and so much internal coherence, that they are worthy of study.
Non-Euclidean geometry resolves our uncertainty about the fifth postulate by replacing it with pluralism—a willingness to gear truth to the worlds we choose to occupy, or the perspectives we choose to take. In Nietzsche’s words, “There is only a perspective seeing, only a perspective ‘knowing’… the more eyes, different eyes, we can use to observe one thing, the more complete will our ‘concept’ of this thing, our ‘objectivity’ be.” By embracing other possible worlds of geometry, we gain a better understanding of geometry as a whole.
Pluralism is harder to swallow in some other branches of mathematics. Consider the nonnegative integers, also known as the whole numbers. The basic properties of the integers do not seem to admit any uncertainty. For example, an integer is prime if it can’t be written as the product of smaller integers: 7 and 11 are prime, but 15 is not, because 15 = 3×5. Euclid proved that there are infinitely many prime numbers. Although we don’t have room for it here, his proof is delightful, and anyone familiar with division and remainders can understand it.
It’s a short step, however, from Euclid to the boundaries of mathematical knowledge. Certain kinds of prime numbers place us in unfamiliar territory once again, on the brink of uncertainty. A Mersenne prime is a power of 2, with 1 subtracted from it. The first few of these are,
22 – 1 = 2 × 2 – 1 = 3
23 – 1 = 2 × 2 × 2 – 1 = 7
25 – 1 = 2 × 2 × 2 × 2 × 2 – 1 = 31
Are there infinitely many Mersenne primes? The largest prime we know of today is 282,589,933 − 1, which has about 25 million digits. The sequence of Mersenne primes seems to go on forever, but we have no proof of this yet. But whether or not we can prove it, surely this claim is either true or false. Either these numbers go on forever, or they don’t. The truth is out there. It has nothing to do with what we poor humans think.
Why is it so hard to be pluralists when it comes to the integers? Why can’t we take the freewheeling attitude that we took toward Euclid’s fifth postulate, responding to questions about straight lines with a cheerful, “Well, it depends on what you call a straight line”? Could there be alternate worlds for the integers as well, some in which the Mersennes go on forever, and others in which they stop?
Like geometry, arithmetic and algebra can have alternate worlds. We could decide that the symbol 7 means something different, or that addition and multiplication work differently. In certain alternate systems of arithmetic, numbers could curve back on themselves like the surface of the Earth instead of marching off to infinity, and x + y might not equal y + x.
But here’s the rub: only one of these worlds is the real one. Only one corresponds to the arithmetic that we know and love. If you ask a mathematician whether she thinks the Mersenne primes are infinite, she will know what you mean; she won’t ask you to define your terms. The integers are so concrete and rigid that they seem to exist independently of our ability to describe them. Surely 7 was prime long before humans came along to think about it, and it will continue to be prime long after we are gone.
One way to justify this sense that the integers are solid and objective is to think in terms of computation. Consider a machine that looks for Mersenne primes. It tries larger and larger powers of 2, subtracts 1 from each one, and checks to see if the result is prime or not. Whenever the result is a prime, it rings a bell. Will that bell continue to ring indefinitely into the future, no matter how long the machine has been running, or will there be some final time after which it will never ring again?
There is nothing fantastical about this machine. You could build it out of electronic parts, or out of wooden gears and Legos, or you could use one of Alan Turing’s machines that reads and writes simple symbols on a paper tape. Admittedly you would need to provide it with an endless supply of energy and paper and avoid the heat death of the universe, but this is no greater an idealization than the frictionless world of Newtonian mechanics. If you grant that much, either the bell will ring forever or it won’t. We might not know which is true, but there is a fact of the matter. (Some readers will dig in their heels at this point and argue that the finite span of the universe—and of our lives—makes any claims about infinity nonsensical. Indeed, there are “finitists” who think that not all the integers exist, or at least not all at once, or even that only those numbers that exist are those that we will have time to write down and think about. We refuse to live in such an impoverished, solipsistic world.)
The stance that mathematical objects exist independent of human thought or experience is an example of realism or Platonism. In Book VII of Plato’s Republic, Socrates tells us that discovering the truth is like stepping into daylight after a lifetime in darkness. The truth is like the sun—it’s out there, singular and illuminating. For the most part, however, we live in a cave surrounded by images, mere representations of things that are real and external. For Plato and the Platonist, the point of thinking is to escape the world of mere appearances and to see truth as it truly is.
Of course, just as in moral philosophy, a debate continues to rage about whether mathematics is a series of discoveries revealing objective truths, or merely a human invention. But we don’t have to believe in some astral plane of existence inhabited by integers, perfect circles, and the like. To be a “pragmatic Platonist” like the American logician Martin Davis, we just have to believe that some mathematical questions have answers—that some things really are true and that the job of mathematics is to figure out what these are. We possess Nietzsche’s will to truth precisely because we believe there is a truth to find.
If we are Platonists about mathematics, if the truth is out there, how can we perceive it? And can such truth ever really be grasped? Computers are powerful tools in the search for examples and counterexamples to our conjectures, revealing tantalizing patterns in complex systems. For this reason, empirical mathematics is of increasing importance throughout the sciences.
But to see all the way to infinity, we need a proof—that old gold standard. As every mathematician knows, achieving this standard can be hard, even for things that seem obviously true. Is there a complete system for doing mathematics that can prove every truth and settle every question? Or are there some questions we can never answer, as the physiologist Emil du Bois-Reymond argued in a speech to the Prussian Academy of Sciences in 1880, questions about which we can only say ignoramus et ignorabimus—we do not know, and we will never know?
The German mathematician David Hilbert (1862–1943) found the idea of ignorabimus intolerable. He attacked it as a “fall of culture” and asserted that every question in mathematics and science had an answer. Hilbert thundered, Wir müssen wissen—wir werden wissen: we must know—we will know. His will to truth was absolute.
Hilbert and the other titans of late-19th- and early-20th-century mathematics formulated a list of basic postulates, or axioms, on which they hoped all of mathematics could be built—axioms powerful enough to prove all true statements while not mistakenly “proving” any false ones. This turns out to be a subtle enterprise, for these axioms have to capture all the forms of logical and mathematical reasoning we have grown accustomed to—proofs by contradiction, by induction, and so on—while avoiding paradoxes and inconsistencies.
If our axioms allow us to define mathematical objects too freely, we can easily fall into paradox. One of the most basic objects in mathematics and logic is a set—the set of six-legged insects, the set of blue things, the set of even numbers, and so on. How about the set of mathematical objects mentioned in this essay? This set includes lines, angles, and Mersenne primes. But it also includes itself, since we just mentioned it.
Now Bertrand Russell comes along and asks us about the set S of all sets that don’t include themselves. Does S include itself or not? If it does, then—by its own definition—it doesn’t. But if it doesn’t, then—again by definition—it does. (You may have heard a more colloquial version of this paradox, involving a barber who shaves those who don’t shave themselves.) Somehow the act of defining S has gotten us into trouble by creating a statement, “S includes itself,” which is both true and false, or maybe neither.
We can’t allow a paradox like this to lurk at the heart of mathematics. Our system must be consistent—it must never contradict itself and never provide “proofs” that something is both true and false. As Hilbert wrote, “If mathematical thinking is defective, where are we to find truth and certainty?” But more positively, paradoxes create a delicious form of uncertainty, forcing us to reexamine the basic building blocks of thought. As Niels Bohr said in the early days of quantum mechanics, “How wonderful that we have met with a paradox. Now we have some hope of making progress.”
By the 1920s, mathematicians had begun to heal the breach that Russell had revealed, arriving at what appeared to be a satisfactory set of axioms, known as ZFC. Z stands for the German logician and mathematician Ernst Zermelo, F for the German-born Israeli mathematician Abraham Fraenkel, and C for the axiom of choice, a particular way to define infinite sets. ZFC lets us talk about everything from arithmetic to infinity while avoiding paradoxes like Russell’s—in particular, by not allowing us to discuss sets that include themselves. As far as we know, ZFC never contradicts itself or produces falsehoods. Although there are alternatives, it is generally accepted as the default foundation of modern mathematics.
But even a good set of axioms does not remove uncertainty from mathematics. A formal proof is a series of steps, each of which combines previous steps according to one of the axioms, until the final goal is reached and we announce, QED. But this series can be long and complicated. Even if we have a finite set of axioms, the number of possible proofs is infinite. How can we search this infinite space?
In 1928, Hilbert posed the Entscheidungsproblem, or “decision problem.” He asked for a general procedure to decide whether a mathematical statement is true or, more precisely, whether it can be proved from a set of axioms. He stipulated that this procedure should be something that we can carry out in a finite number of reliable steps, without leaps of intuition—in modern terms, the way a computer program or algorithm operates. If such a procedure exists, and if its axioms are powerful enough to prove all truths, then mathematics would be complete. We would finally know.
In the 1930s, Hilbert’s dream was rudely interrupted. First, in 1931 the Austrian logician Kurt Gödel proved that there were unprovable truths. Specifically, he showed that any axiomatic system powerful enough to talk about the integers could also express the paradoxical statement, “This sentence can’t be proved.” Either this sentence can be proved or it can’t. If it can be proved, then it is false—but then we have “proved” a falsehood. So if our axioms never prove false things, this sentence can’t be proved, just as it claims—making it true but unprovable.
Admittedly, we are playing fast and loose with two different concepts here: whether an axiomatic system is sound (it never proves a falsehood) versus whether it is consistent (it never contradicts itself). Soundness requires a notion of truth that is external to the system—which a Platonist would heartily endorse—whereas consistency can be defined inside the system. Gödel was a Platonist, but he carefully phrased his argument in terms of consistency: if his sentence can be proved, then we have by definition proved its opposite as well, and the system has contradicted itself.
All of this may seem like a verbal game, but Gödel’s unprovable truths are not idle paradoxes. They are concrete statements about the integers, different in degree but not in kind from the statement that there are infinitely many Mersenne primes. His incompleteness theorem shows that no finite set of axioms can prove all true statements about the integers, unless it mistakenly proves some false ones as well.
At a minimum, Hilbert wanted to prove that mathematics was consistent and would never contradict itself. Gödel put even this modest goal out of reach with his second incompleteness theorem, which states that no axiomatic system can prove its own consistency. We can’t use ZFC to prove that ZFC will never blow up in our faces, proving that something is both true and false. To prove that our mathematical foundation is sound, we will always have to use some kind of higher-level reasoning. No finite foundation can give us the certainty we crave: the foundation must be supported from above.
The blows kept coming. In 1936, Alan Turing proved that we couldn’t even tell which statements could be proved. If we want to know whether our favorite mathematical statement has a proof, we can build a machine like the Mersenne prime searcher that looks for longer and longer proofs, and program it to halt if it ever finds one. Turing called the question of whether a machine (or computer program) would ever halt, as opposed to running forever, the “halting problem.” If we can solve the halting problem for this proof searcher, we can solve Hilbert’s Entscheidungsproblem.
Of course, if we run this machine and it does indeed halt, we have our proof. But if it runs for a billion years and still hasn’t found a proof, we have no idea whether it ever will. If only we could tell whether a machine will halt someday, without having to run it forever! But if we could do that, we would have a paradox. We could build a machine that predicts its own behavior and then does the opposite, halting if it will run forever and running forever if it will halt. The only escape from this paradox is to accept that no general halt-predicting machine exists. There is no algorithm for the halting problem: it is undecidable, and so is Hilbert’s Entscheidungsproblem. With enough work, we might achieve certainty about some mathematical questions, but no general method—or machine—can provide that certainty for us.
The same argument shows that, for at least some of Turing’s machines, the fact that they will run forever is an unprovable truth. To see this, suppose that all truths of the form “this machine will run forever” were provable. If that were true, we could solve the halting problem for any machine by doing two things simultaneously: running the machine to see whether it halts, and looking for longer and longer proofs that it never will. Unless the fact that it never halts is sometimes unprovable, one of these two methods will always yield the answer. Thus Turing’s undecidable problems and Gödel’s unprovable truths are intimately related.
In 2016, the computer scientists Adam Yedidia and Scott Aaronson devised a Turing machine that searches for contradictions in ZFC. According to Gödel’s second incompleteness theorem, ZFC can’t prove its own consistency. Thus, while we fervently hope that this search for contradictions would be in vain and that this machine would run forever, ZFC can’t prove that it would.
Unprovability, undecidability, uncomputability—these are defeats for Hilbert’s program, and they seem like defeats for mathematics itself. How can we pursue truth if every tool we have for that pursuit is flawed? Is there even a truth to pursue?
These may indeed be defeats for a naïve and rigid notion of certainty. But we argue that they are actually triumphs of the human intellect’s ability to work through intractable questions and better understand when and to what extent these questions can be resolved. Indeed, many of today’s mathematicians and computer scientists view these negative results in a positive light. No machine will do our mathematics for us, but would we want it to? Shouldn’t mathematics, like everything that matters, be an arena in which the full force of creativity and intuition must be brought to bear?
The mathematical community took some time to digest the work of Gödel and Turing, and several decades passed before this positive spin emerged. But already in 1944, just eight years after Turing’s proof, the logician and mathematician Emil Post wrote, “The conclusion is unescapable that even for such a fixed, well-defined body of mathematical propositions, mathematical thinking is, and must remain, essentially creative.” In 1952, the British mathematician John Myhill followed up with:
Negatively this discovery means that no matter what changes and improvements in mathematical technique the future may bring, there will always be problems for whose solution those techniques are inadequate; positively, it means that there will
always be scope for ingenuity and invention in even the most formalized of disciplines.
Mathematics will never be complete. No machine or axiomatic system can tell the entire story. But this uncertainty is not a source of despair—it is the most essential part of being human, the boundary of our finitude. We are limited beings, but these limits are meant to be faced and transcended.
Platonism seems to fit our understanding of the integers and computer programs, but we have reason to be far less confident in the more remote branches of mathematics. Consider the set of all real numbers: not just numbers we can name, like ⅔ or , but the entire number line you drew in school, with every possible sequence of digits after the decimal point. In 1874, the German mathematician Georg Cantor proved that there are more real numbers than there are integers. Both sets are of infinite size, but one is more infinite than the other.
In 1878, Cantor put forward the “continuum hypothesis.” It states that there are no sizes of infinity between these two: that the continuum of real numbers is the smallest set bigger than the set of all integers. (The alert reader may point out that the set of rational numbers—fractions such as ½, ⅔, 17⁄10, and so on—includes all the integers but not all the reals, so it seems to lie in between those two sets. But there is a way to line up the integers and the rationals with each other such that each integer corresponds to a rational and vice versa. Thus these two sets are actually the same infinite size.) Cantor, however, was unable to find a proof. At the outset of the 20th century, this was considered one of the leading open questions in mathematics, appearing at the top of a list of problems that David Hilbert presented to the International Congress of Mathematicians in 1900. Over the next decades, many of the great logicians and set theorists tried to prove or disprove it.
Gödel was one of those who believed that the continuum hypothesis was false. But in 1940, he proved that it couldn’t be disproved using the standard axioms of set theory, namely ZFC, and in 1963 the American mathematician Paul Cohen showed that it couldn’t be proved from ZFC either. We really can have it both ways: there are many consistent pictures of infinity. In some, there is no intermediate infinity between the reals and the integers. In others, there is one, or even infinitely many. The standard axioms simply do not exclude either possibility: we say that the continuum hypothesis is independent of the axioms.
One might have several reactions to this. Gödel was delighted by Cohen’s proof of independence. But since he was also a Platonist, he felt that questions about infinite sets had answers, as surely as do questions about the integers. Either the continuum hypothesis is true or it is false. If the standard axioms can’t settle it either way, let’s look for stronger axioms that will.
We could adopt a pluralistic attitude instead and conclude that we can think about infinity in many ways. Unlike with the bell-ringing Mersenne-searching machine, there is no conceivable physical system whose behavior depends on whether the continuum hypothesis is true or not: infinity is not subject to experiment. Cohen’s work was based on a new technique called “forcing,” which allows set theorists to create a wide variety of possible worlds. As with non-Euclidean geometry, as long as these worlds are beautiful and interesting, we can embrace all of them. Perhaps the realm of the infinite is more like religion than physics. Perhaps it has no singular truth shining like Plato’s sun, and we should let our fellow humans believe what they like.
Our will to truth is often frustrated, even in the crystal world of mathematics, where we might expect certainty to rule. Hilbert’s hopes for a complete system that would provide truth once and for all were irrevocably dashed by Gödel and Turing.
But we have not reacted by abandoning the search for truth—quite the opposite. This search has revealed a rich array of mathematical worlds, with different methods of proof, different axioms, and different visions of infinity. None of these alternate worlds captures all of mathematical truth. Each one offers a perspective, and in their plurality they hint at the whole. Thus one might say that modern mathematics has moved us from Platonism to pluralism.
But this pluralism is not an empty relativism, where we agree to disagree and go our separate ways, as if we have nothing to say to each other. Neither is it a nihilistic relativism where we declare that it’s all nonsense anyway, then retreat to our separate bubbles muttering about “alternative facts” and “fake news.” It is more akin to the active, vibrant pluralism of a civil society, where we work to understand each other’s ways of thinking, explore our similarities and differences, and seek common ground. It requires us to respect each other’s views but insists on our right to question them. It admits our ignorance while remaining optimistic that we can learn more. It insists that there is a truth that we can and should pursue together—but that this pursuit is endless, with uncertainty our constant companion.

